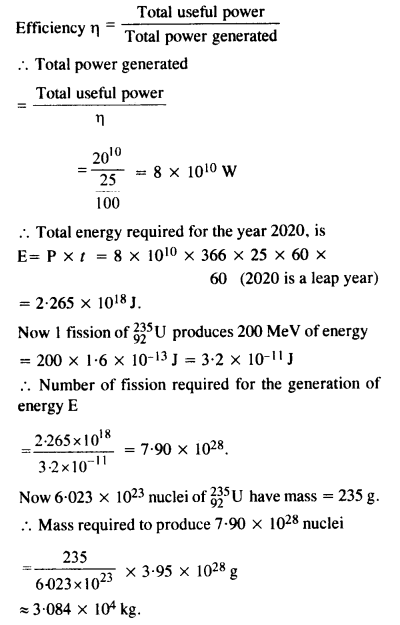NCERT Solved Exercise Questions – Class 12 Physics Chapter 13 Nuclei
13.1 (a) Two stable isotopes of lithium 6 3 Li and 7 3 Li have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes, 10 5B and 11 5B. Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of 10 5B and 11 5 B.
Ans – Mass of lithium isotope , m1 = 6.01512 u
Mass of lithium isotope , m2 = 7.01600 u
13.2 The three stable isotopes of neon: 20 21 22 10 10 Ne, Ne and Ne 10 have respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u, respectively. Obtain the average atomic mass of neon.
Ans – Atomic mass of , m2 = 20.99 u
Abundance of , η2 = 0.27%
Atomic mass of , m3 = 21.99 u
Abundance of , η3 = 9.22%
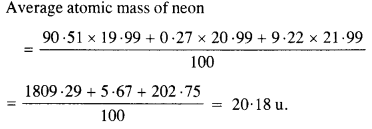
13.3 Obtain the binding energy (in MeV) of a nitrogen nucleus ( ) 14 7 N , given m ( ) 14 7 N =14.00307 u
Ans – Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn= 1.008665 u
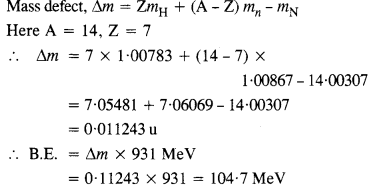
13.4 Obtain the binding energy of the nuclei 56 26Fe and 209 83 Bi in units of MeV from the following data:
m ( 56 26Fe ) = 55.934939 u m ( 209 83 Bi ) = 208.980388 u
Ans – Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
13.5 A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of 63 29Cu atoms (of mass 62.92960 u).
Ans – Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm’ = 29 × 1.007825 + 34 × 1.008665 − 62.9296
= 0.591935 u
13.6 Write nuclear reaction equations for
(i) α-decay of 226 88 Ra
(ii) α-decay of 242 94 Pu
(iii) β– -decay of 32 15 P
(iv) β– -decay of 210 83 Bi
(v) β+ -decay of 11 6 C
(vi) β+ -decay of 97 43 Tc
(vii) Electron capture of 120 54 Xe
Ans – This is a helium nucleus. – An electron (e for atom, and e+ for atom plus) is a nucleiand. A loss of two protons and four neutrons occurs in every -decay. A neutrino and one proton are lost in every +-decay, and the nucleus releases one. An antineutrino is emitted from the nucleus along with a gain of 1 proton in every -decay.
The various nuclear reactions for the situations above can be expressed as follows:
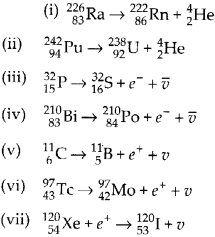
13.7 A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to
a) 3.125%,
b) 1% of its original value?
Ans – T years is the radioactive isotope’s half-life.
The radioactive isotope’s original concentration was N0.
- Following decay, the radioactive isotope’s quantity equals N.
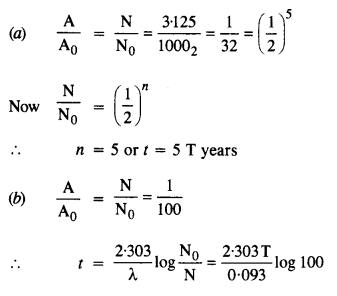
13.8 The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive 14 6 C present with the stable carbon isotope 12 6 C . When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of 14 6 C , and the measured activity, the age of the specimen can be approximately estimated. This is the principle of 14 6C dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
Ans – Living carbon-containing stuff decays at a rate of 15 decays per minute (R).
Let N represent the total number of radioactive atoms in a typical carbon-containing substance.
13.9 Obtain the amount of 60 27Co necessary to provide a radioactive source of 8.0 mCi strength. The half-life of 60 27Co is 5.3 years.
Ans – The radioactive source’s potency is shown as follows:
8.0mCi = dN/dt
Where,
N is the quantity of atoms needed.
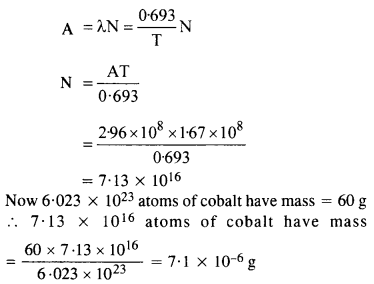
13.10 The half-life of 90 38Sr is 28 years. What is the disintegration rate of 15 mg of this isotope?
Ans – Half life of , 
= 28 years
= 28 × 365 × 24 × 60 × 60
= 8.83 × 108 s
13.11 Obtain approximately the ratio of the nuclear radii of the gold isotope 197 79 Au and the silver isotope 107 47 Ag .
Ans – Gold mass number: AAu = 197
Silver mass number is 107 (AAg).
The following relationship exists between the two nuclei’s mass numbers and their ratio of radii:
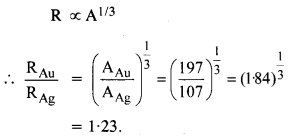
13.12 Find the Q-value and the kinetic energy of the emitted α-particle in the α-decay of
(a) 226 88 Ra and
(b) 220 86 Rn .
Given m ( 226 88 Ra ) = 226.02540 u, m ( 222 86 Rn ) = 222.01750 u, m ( 220 86 Rn ) = 220.01137 u, m ( 216 84 Po ) = 216.00189 u.
Ans – Alpha particle decay of 
emits a helium nucleus. As a result, its mass number reduces to (226 − 4) 222 and its atomic number reduces to (88 − 2) 86. This is shown in the following nuclear reaction.
13.13 The radionuclide 11C decays according to 11 11 + 6 5 C B+ + : =20.3 min → e T ν 1/2 The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values:
m ( 11 6 C) = 11.011434 u and m ( 11 6B ) = 11.009305 u,
calculate Q and compare it with the maximum energy of the positron emitted.
Ans – Maximum energy possessed by the emitted positron = 0.960 MeV
The change in the Q-value (ΔQ) of the nuclear masses of the
nucleus is given as:
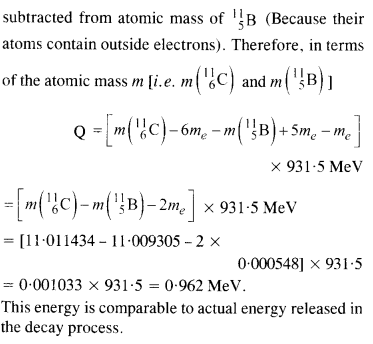
13.14 The nucleus 23 10 Ne decays by β– emission. Write down the β-decay equation and determine the maximum kinetic energy of the electrons emitted.
Given that:
m ( 23 10 Ne ) = 22.994466 u m ( 23 11 Na ) = 22.989770 u.
Ans –
The emitted nucleus is way heavier than the 
particle and the energy of the antineutrino is also negligible and therefore the maximum energy of the emitted electron is equal to the Q value.The emitted nucleus is way heavier than the particle and the energy of the antineutrino is also negligible and therefore the maximum energy of the emitted electron is equal to the Q value.
13.15 The Q value of a nuclear reaction A + b → C + d is defined by Q = [ mA + mb – mC – md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
(i) 13 2 2 11 1 1 H+ H H+ H →
(ii) 12 12 20 4 6 6 10 2 C+ C Ne+ He → Atomic masses are given to be m ( 2 1 H ) = 2.014102 u m ( 3 1 H ) = 3.016049 u m ( 12 6 C ) = 12.000000 u m ( 20 10 Ne ) = 19.992439 u
Ans – The given nuclear reaction is:
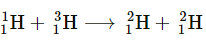
It is given that:
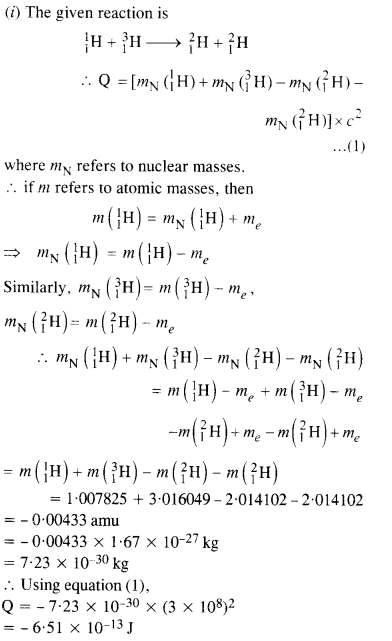
13.16 Suppose, we think of fission of a 56 26Fe nucleus into two equal fragments, 28 13 Al . Is the fission energetically possible? Argue by working out Q of the process. Given m ( 56 26Fe ) = 55.93494 u and m ( 28 13 Al ) = 27.98191 u.
Ans – The fission of
can be given as:
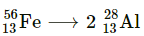
It is given that:
13.17 The fission properties of 239 94 Pu are very similar to those of 235 92 U . The average energy released per fission is 180 MeV. How much energy,in MeV, is released if all the atoms in 1 kg of pure 239 94 Pu undergo fission?
Ans – Amount of pure
, m = 1 kg = 1000 g
NA= Avogadro number = 6.023 × 1023
Mass number of= 239 g
13.18 A 1000 MW fission reactor consumes half of its fuel in 5.00 y. How much 235 92 U did it contain initially? Assume that the reactor operates 80% of the time, that all the energy generated arises from the fission of 235 92 U and that this nuclide is consumed only by the fission process.
Ans – the fission of one nucleus of 23592U, energy generated is 200 MeV
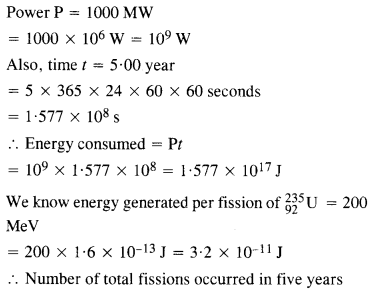
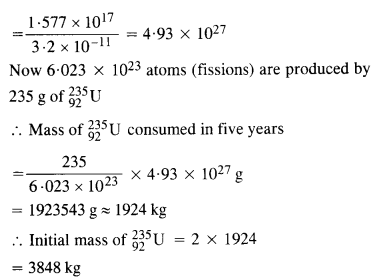
13.19 How long can an electric lamp of 100W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as 22 3 11 2 H+ H He+n+3.27 MeV →
Ans – Amount of deuterium, m = 2 kg
1 mole, i.e., 2 g of deuterium contains 6.023 × 1023 atoms.
13.20 Calculate the height of the potential barrier for a head on collision of two deuterons. (Hint: The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm.)
Ans – Radius of 1st deuteron + Radius of 2nd deuteron
Radius of a deuteron nucleus = 2 fm = 2 × 10−15 m
∴d = 2 × 10−15 + 2 × 10−15 = 4 × 10−15 m
13.21 From the relation R = R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e. independent of A).
Ans – R = R0A1/3
Where,
R0 = Constant.
A = Mass number of the nucleus
13.22 For the β+ (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K–shell, is captured by the nucleus and a neutrino is emitted).
1 A A eX Y Z Z ν + +→ + − Show that if β+ emission is energetically allowed, electron capture is necessarily allowed but not vice–versa.
Ans –
This means that if Q1 > 0, then Q2 > 0, but vice versa isn’t always possible.
Therefore, positron emission can occur without electron capture.
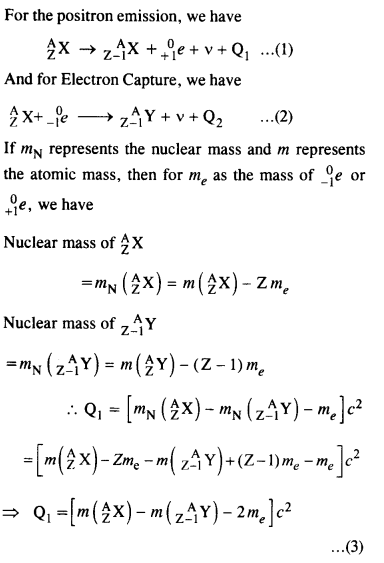
13.23 In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are 24 12Mg (23.98504u), 25 12Mg (24.98584u) and 26 12Mg (25.98259u). The natural abundance of 24 12Mg is 78.99% by mass. Calculate the abundances of other two isotopes.
Ans –Average atomic mass of magnesium, m = 24.312 u
13.24 The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei 41 20Ca and 27 13Al from the following data: m( 40 20Ca ) = 39.962591 u m( 41 20Ca ) = 40.962278 u m( 26 13Al ) = 25.986895 u m( 27 13Al ) = 26.981541 u
Ans – E = Energy equivalent of total mass afterward – Energy equivalent of nucleus before can be used to calculate the Ca’s neutron separation.
13.25 A source contains two phosphorous radio nuclides 32 15P (T1/2 = 14.3d) and 33 15P(T1/2 = 25.3d). Initially, 10% of the decays come from 33 15 P. How long one must wait until 90% do so?
Ans – In the mixture of P-32 and P-33 initially 10% decay came from P-33. Hence initially 90% of the mixture is P-32 and 10% of the mixture is P-33. Let after time’t’ the mixture is left with 10% of P-32 and 90% of P-33. Half life of both P-32 and P-33 are given as 14.3 days and 25.3 days respectively. Let V be total mass undecayed initially and ‘y’ be total mass undecayed finally. Let initial number of P-32 nuclides = 0.9 x Final number of P-32 nuclides = 0.1 y Similarly, initial number of P-33 nuclides = 0.l x Final number of P-33 nuclides = 0.9 y For isotope P-32
13.26 Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes: 223 209 14 88Ra Pb C
223 219 4 88Ra Rn He → + 86 2 Calculate the Q-values for these decays and determine that both are energetically allowed.
Ans – Mass of
m1 = 223.01850 u
Mass of
m2 = 208.98107 u
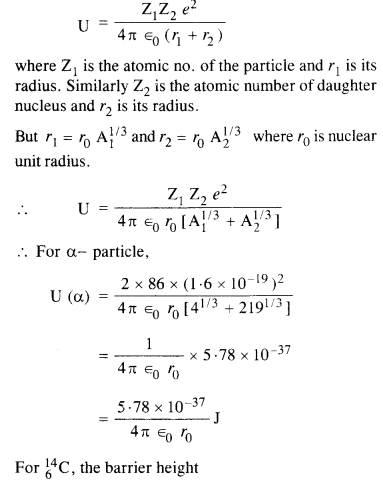
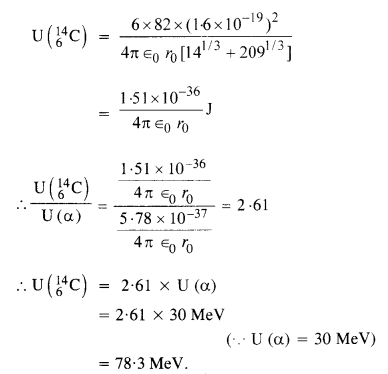
13.27 Consider the fission of 238 92U by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are 140 58Ce and 99 44Ru. Calculate Q for this fission process. The relevant atomic and particle masses are m( 238 92U ) =238.05079 u m( 140 58Ce ) =139.90543 u m( 99 44Ru ) = 98.90594 u
Ans – Mass of a nucleus
m1 = 238.05079 u
Mass of a nucleus 
m2 = 139.90543 u
Mass of a nucleus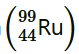
, m3 = 98.90594 u
13.28 Consider the D–T reaction (deuterium–tritium fusion) 23 4 11 2 H H He n +→ +
(a) Calculate the energy released in MeV in this reaction from the data: m( 2 1H )=2.014102 u m( 3 1H ) =3.016049 u
(b) Consider the radius of both deuterium and tritium to be approximately 2.0 fm.
What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzman’s constant, T = absolute temperature.)
Ans – Calculate the energy released in MeV in this reaction from the data:
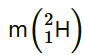= 2.014102 u
13.29 Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 13.6. You are given that m( 198Au) = 197.968233 u m( 198Hg) =197.966760 u
Ans – Calculate the energy released in MeV in this reaction from the data:
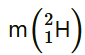= 2.014102 u
13.30 Calculate and compare the energy released by a) fusion of 1.0 kg of hydrogen deep within Sun and b) the fission of 1.0 kg of 235U in a fission reactor.
Ans – (a) Amount of hydrogen, m = 1 kg = 1000 g
1 mole, i.e., 1 g of hydrogen 
contains 6.023 × 1023 atoms.
13.31 Suppose India had a target of producing by 2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i.e. conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission of 235U to be about 200MeV.
Ans – Amount of electric power to be generated, P = 2 × 105 MW
10% of this amount has to be obtained from nuclear power plants.
∴Amount of nuclear power,
